This document, created in 1998, is a very partial translation into English of the Annex 2 of my PhD thesis. In 2000, I began the implementation of WebKB-2, a shared knowledge server, and realised that the ontology sharing protocols I described in the Annex 2 of my PhD thesis were too complex for people to adopt them. Hence, I implemented a more restricted but simpler approach to handle the sharing of the taxonomy, and I also extended it to take any statement (i.e. not just subsumption links) into account.
Here, "term" refers to a "formal term", i.e. an identifier for a category (type or individual).
A user Ux may modify the terms s/he has created.
A user Ux may add definitions to his/her terms unless this leads to an unrepairable inconsistency with specialising statements S created by other users. The inconsistency may be detected by Ux or the system. To repair the inconsistency, Ux may do some modifications on S in a transaction or accept the system proposals: Ux may modify his/her terms in S or contextualise the s in S.
Ux may add any fact (including specialisations or generalisations of Uz fact) if that doesn't lead to an inconsistency.
To solve an inconsistency, Ux may modify a fact of Uz by generalising, specialising or contextualising it. Uz notified of modification and its cause.
Ux may add a definition to a term of Uz or reuse it or specialise it or generalise it unless that leads to an inconsistency with a statement co-created by Ux.
If that leads to an inconsistency (that the system or s/he detects)
even if s/he hasn't created it, unless this leads to a detectable inconsistency
that the user or the system can detect but cannot repair.
We detail in the next section how some inconsistencies can be repaired.
??? When a user adds a definitional relation to a term t, s/he becomes
co-creator of this term. If the definitional relation is a generalisation
relation, the user also becomes co-creator of the terms generalising t at the
momment of the creation of the relation.???
To create a new term, a user must specialise or generalise another term. This ensures that all terms can be compared and supports the application of the following rules.
A user may not remove a term directly but s/he may try to remove a relation between it and one of its generalising terms. A term which is no more connected to other terms is removed by the system.
Only the creator of a definitional relation between terms may remove it or modify it. If a user Ux tries to remove a relation which s/he created but which has other co-creators, the relation is not actually removed but is not anymore visible by Ux (and the relation has no creator anymore). If the relation is a specialisation relation, the specialised term is not anymore visible by Ux but its specialisations are still visible by Ux unless s/he asked to remove them too.??????
A user Ux who hasn't created a relation between terms may not remove it but may specify that s/he doesn't want to see it anymore. If the relation is a specialisation relation, the specialised term is not anymore visible by Ux but its specialisations are still visible by Ux unless s/he asked not to display them too.??????
Several cases (exch user may choose what he prefers on his types) but the user which repairs the inconsistency chooses: 1) minimal (no clone), 2) clones (keep definitions)
Automatic inconsistency repairs allows a user Uy to add or modify terms s/he created without being bothered by specialising terms created by other users.
The system must modify the relations of other users to repair the inconsistency. Indeed, Uy cannot wait for other users to correct the way they used the terms of Uy. Besides, the automatic repair may be partially or entirely accepted by the other users.???
to define: term co-created, exclusive link, generalisations, direct generalisations, direct specialisations
If either
a) Y0 and Y1 are exclusive and Uy adds a relation of specialisation between Y2
and Y3 which therefore also makes Z3 a specialisation of Y0 and Y1, or
b) Z3 specialises Y0, Y1, Y2 and Y3, and Uy adds a relation of exclusion
between Y0 and Y1,
then the created inconsistency may be repaired by the system as follows.
The principle is first to "clone" one of the terms generalising Z3 and created
by Uy, that is to replace it by a term (called the "clone") which has the same
generalisations as the cloned term except the ones which cause the
inconsistency.
Thus, Z3 has the same definitions as before the removal of the relation between Y5 and Z5 except those creating the inconsistency.
Thus the inconsistency repairing is a contrainst relaxation operation.
Thanks to that, a user Uy may relate terms s/he created without bothering
about specialising terms created by other users. These specialising terms
may even be invisible for Uy (but the system takes all terms into account
to maintain the consistency of the KB).
The users which have been registered as creators of the terms and relations
created by the system to fix inconsistency are notified and may create
more adequate relations or give the new terms more adequate names.????
If when a user Uy adds or modifies a definition to a term Y0 s/he created, the system detects an inconsistency caused by the existence of a set Ez of terms specialising Y0 and created by users other than Uy, then the created inconsistency may be repaired by the system as follows.
As before, the principle is a constraint relaxation via term cloning.
Now, the cloned terms are the term Y0 plus, in some cases, some of the
terms which specialises Y0 (the cloning method is different from before).
The next figure illustrates the method which is described afterwards.
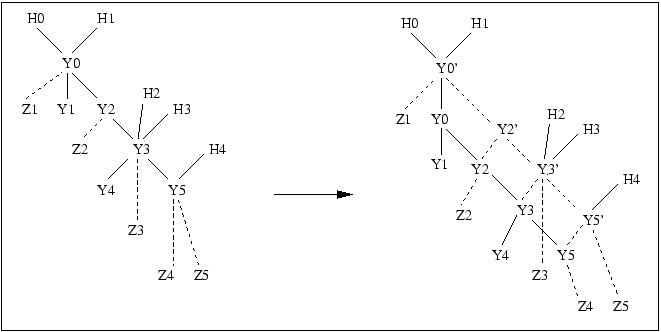
| Ez={Z1,Z3,Z5}. Uy has just added a definition to Y0 and this definition is inconsistent with the definitions of the terms Z1, Z3 and Z5 which have not been created by Uy. |
The inconsistency is fixed. The system has created the terms Y0', Y2', Y3' and Y5' respectively equivalent to Y0, Y2, Y3 and Y5 before the adding of the new definition to Y0. |
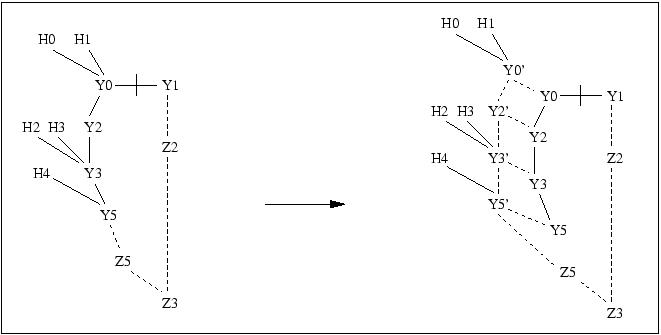
| Ez={Z3,Z5} or Ez={Z2,Z3}. Z3 specialises the exclusive terms Y0 and Y1. Y0, Y1, Y2, Y3 and Y5 have been created by Uy while Z1, Z3 and Z5 have been created by Uz (specialisation relations leading to terms created by Uz are dashed). |
The inconsistency is fixed. To do that, Ez={Z3,Z5} has been chosen and the system has created Y5' by cloning Y5 (and registered Uz as its creator) and replaced the relation between Z5 and Y5 by the relation between Z5 and Y5' (another option would be to ask Uy or Uz if s/he prefers Y1 to be cloned instead of Y5). |
As in the previous case, the operations of cloning and replacement of
relations are constraint relaxations operations.
The registered creators of the new terms and relations are the creators of
the terms of Ez.
If a clone is necessary for repairing inconsistencies created by several
terms of Ez, only one of the creators of these terms becomes creator
of the clones, the other creators become co-creators of the clones.
The creators of the terms of Ez are not anymore co-creator of Y0 and of the
cloned terms.
For the creator and co-creators of Y0' and the clones, the name of Y0' and
these clones will appear as the name of Y0 and the cloned terms
but prefixed by the string "clone_of_".